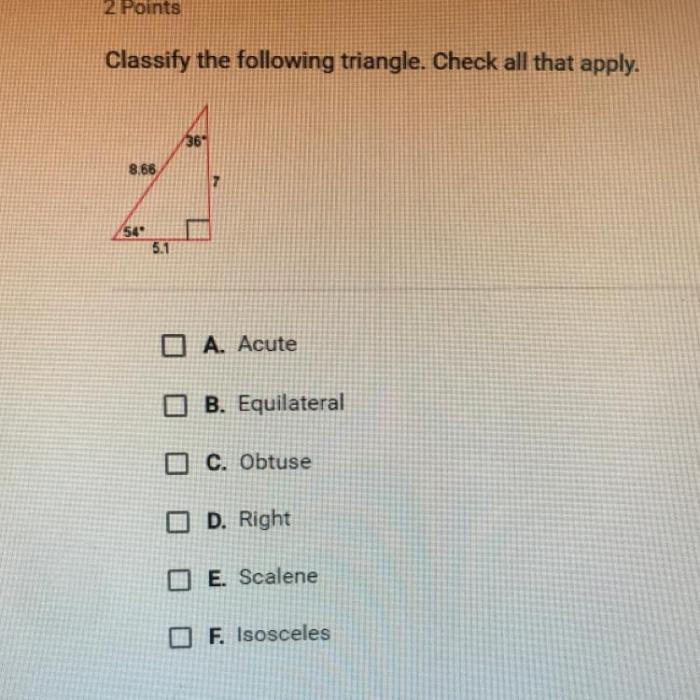
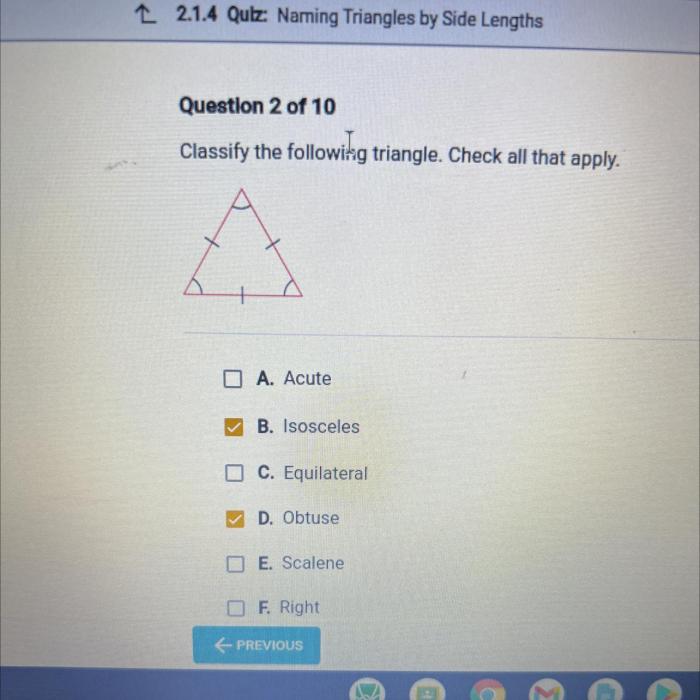
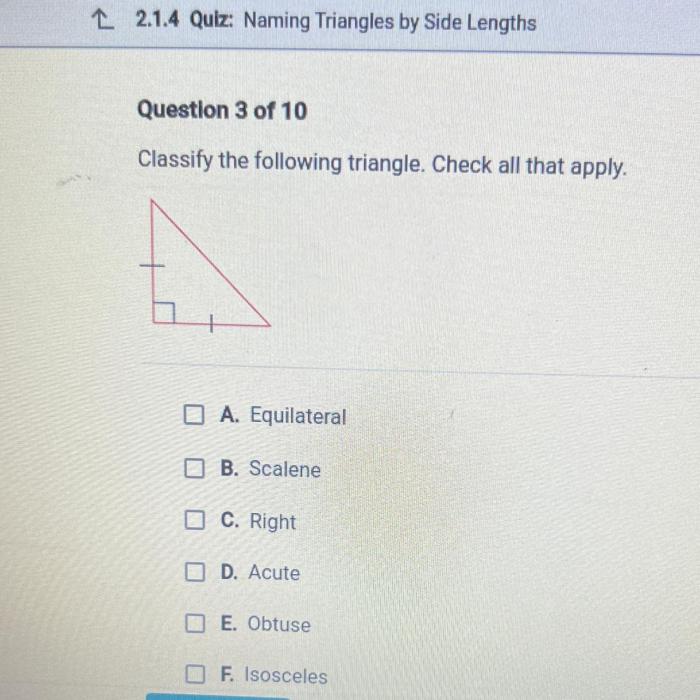
Classify the following triangle check all that apply apex – Triangle classification, a fundamental concept in geometry, involves categorizing triangles based on their side lengths and apex. Understanding the apex’s significance and its role in triangle classification is crucial for comprehending the properties and characteristics of these geometric shapes.
This comprehensive guide explores the various types of triangles, their apex locations, and the criteria used for classification. Through detailed explanations and illustrative examples, we delve into the intricacies of triangle geometry, providing a deeper understanding of these essential concepts.
Triangle Classification: Classify The Following Triangle Check All That Apply Apex
Triangles are classified into different types based on the lengths of their sides. The three main types of triangles are:
- Equilateral triangle: All three sides are equal in length.
- Isosceles triangle: Two sides are equal in length, and the third side is different.
- Scalene triangle: All three sides are different in length.
Triangle Apex, Classify the following triangle check all that apply apex
The apex of a triangle is the vertex opposite the base. In an equilateral triangle, the apex is any of the three vertices. In an isosceles triangle, the apex is the vertex opposite the equal sides. In a scalene triangle, the apex is the vertex opposite the longest side.
Triangle Classification by Apex
Triangles can also be classified based on the location of their apex:
- Acute triangle: The apex is less than 90 degrees.
- Right triangle: The apex is 90 degrees.
- Obtuse triangle: The apex is greater than 90 degrees.
| Triangle Type | Apex Location | Properties |
|---|---|---|
| Equilateral | Any vertex | All sides equal, all angles equal to 60 degrees |
| Isosceles | Vertex opposite equal sides | Two sides equal, two angles equal |
| Scalene | Vertex opposite longest side | All sides different, all angles different |
| Acute | Less than 90 degrees | All angles less than 90 degrees |
| Right | 90 degrees | One angle is 90 degrees |
| Obtuse | Greater than 90 degrees | One angle is greater than 90 degrees |
- Example of an equilateral triangle: A triangle with sides of length 3 cm, 3 cm, and 3 cm.
- Example of an isosceles triangle: A triangle with sides of length 5 cm, 5 cm, and 8 cm.
- Example of a scalene triangle: A triangle with sides of length 4 cm, 6 cm, and 8 cm.
- Example of an acute triangle: A triangle with angles of 60 degrees, 70 degrees, and 50 degrees.
- Example of a right triangle: A triangle with angles of 90 degrees, 30 degrees, and 60 degrees.
- Example of an obtuse triangle: A triangle with angles of 100 degrees, 40 degrees, and 40 degrees.
Commonly Asked Questions
What is the apex of a triangle?
The apex is the vertex opposite the base of a triangle.
How many ways can triangles be classified based on their apex?
Triangles can be classified into three types based on their apex: acute, right, and obtuse.
What is the significance of the apex in triangle geometry?
The apex plays a crucial role in determining the properties of a triangle, such as its area, perimeter, and angle measures.